Einfluss der Frässpindel-Orientierung auf die Bearbeitungsgenauigkeit beim Fräsen mit Industrierobotern
Industrieroboter finden zunehmend Anwendung bei Bearbeitungsprozessen. Hier weisen die Roboter bedingt durch ihre vergleichsweise geringe Steifigkeit eine deutlich höhere Abdrängung des Endeffektors, als herkömmliche CNC-Maschinen, auf. Dieser Beitrag stellt einen Ansatz zur Minimierung solcher Abdrängungen des Werkzeugs durch die Ausnutzung der rotatorischen Freiheitsgrade an der Frässpindel vor. Hierzu wurde die Abdrängung des Endeffektors bei unterschiedlichsten Orientierungen der Frässpindel mittels eines Strukturmodells untersucht.
Die Einsatzgebiete für Industrieroboter gehen bereits weit über die klassischen Schweiß-, Montage- und Klebeaufgaben hinaus. So werden Industrieroboter zunehmend in der Metallbearbeitung eingesetzt, wie z. B. beim Blechumformen, Polieren, Entgraten, Bohren, Schleifen und Fräsen [1-3]. Im Gegensatz zu CNC-Maschinen bieten Roboter eine hohe Flexibilität, geringe Investitionskosten pro Kubikmeter Arbeitsraum sowie eine Möglichkeit zur Interaktion mit anderen Maschinen [4]. Demgegenüber steht, bedingt durch den seriellen kinematischen Aufbau, die geringe Steifigkeit des Roboters, was zu einer hohen Abdrängung des Werkzeugs führen kann [5]. Die Roboterstruktur wird beim Fräsen durch die auftretende Aktiv- und Passivkraft mehrachsig belastet, wodurch das Nachgiebigkeitsverhalten des Roboters sich in allen drei Raumrichtungen dynamisch relevant auf das Bearbeitungsergebnis auswirkt [6]. Die auftretenden Abweichungen des Werkzeugpunkts sind auf geometrische Fehler (Nulllage-, Armlängen- und Winkelfehler) und nicht-geometrische Fehler, wie der Gelenkelastizität unter Prozessbelastung, zurückzuführen [7]. Gerade beim Fräsen wirken mitunter hohe Kräfte auf die Roboterstruktur, die zu einer belastungsabhängigen Winkelverdrehung der Gelenke und schlussendlich einer Abdrängung des Werkzeugs führen. Ein entscheidender Grund hierfür sind die in Robotern eingebauten Standardgetriebe, die mit Spiel behaftet sind und nur eine begrenzte Verdrehsteifigkeit aufweisen [8]. Aufgrund der Vielzahl an nachgiebigen Komponenten kann daraus eine Abdrängung des Werkzeugpunkts im Millimeterbereich resultieren [9]. Zur Identifikation der Gelenksteifigkeiten und Kompensation der Abdrängungen werden beispielsweise Stereokamerasysteme [10] oder verschiedene Steifigkeitsmodelle [11] eingesetzt.
Kipp- und Drehsteifigkeit
Die Winkelverdrehungen durch die Ungenauigkeiten in den Gelenken haben einen großen Einfluss auf die Abdrängung des Werkzeugpunkts im dynamischen Fräsprozess. Diese Ungenauigkeiten sind jedoch nicht in allen Wirkrichtungen des Gelenks gleich groß. Die Wirkrichtungen eines Gelenks werden in die Dreh- und die Kipprichtung unterschieden. Die Drehrichtung wird in Richtung der Rotationsachse angenommen und kann mit einer Rotationssteifigkeit definiert werden. Unter der Rotationssteifigkeit c wird im Allgemeinen eine Größe verstanden, die den Widerstand eines Körpers gegen eine Verdrillung ∆φ durch ein Moment M beschreibt:
c= M/∆φ (1)
Unter dem Begriff Kippsteifigkeit wird die Steifigkeit orthogonal zur Rotationsachse verstanden, hier ist aufgrund des deutlich massiveren Aufbaus der Gelenke in Kipprichtung und des nicht vorhandenen Einflusses des Getriebespiels, die Nachgiebigkeit deutlich geringer [5].
Dieser Effekt lässt sich zur Erhöhung der Steifigkeit des Roboters nutzen, indem durch eine Anpassung der Pose die wirkenden Momente in den Gelenken zu einem möglichst großen Teil in Kipprichtung optimiert werden. So ist eine geringere Abdrängung des Werkzeugs zu erwarten. Wie bereits in der Literatur beschrieben [12-14], geschieht dies üblicherweise indem das Werkzeug um seine z-Achse in der Orientierung R_z umorientiert wird, woraus sich eine Vielzahl redundanter Gelenkkonfigurationen für einen Fräspunkt ergeben.
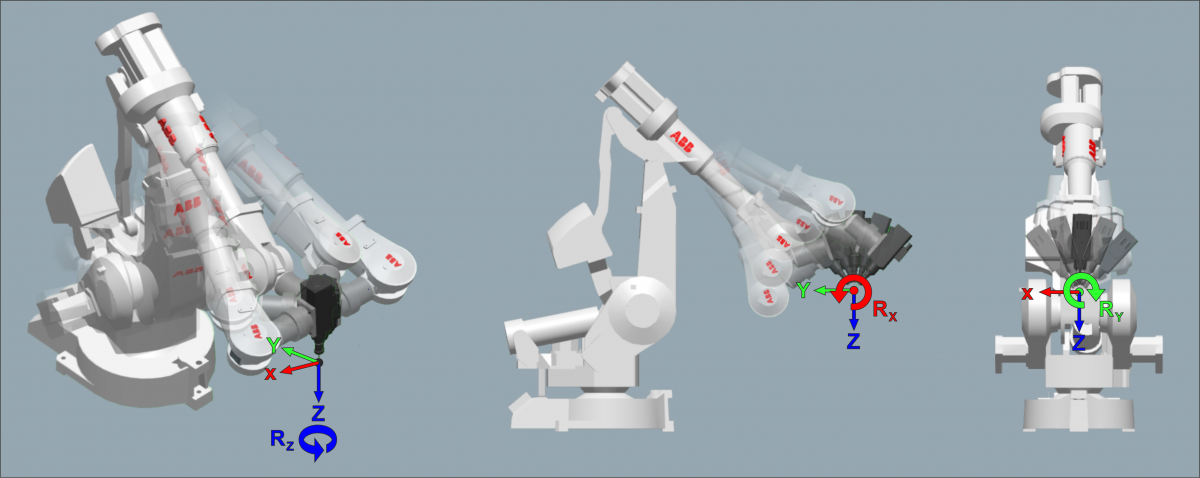
Bild 1: Umorientierung der Frässpindel um die Z- (links), X- (Mitte) und Y-Achse (rechts).
Die im Rahmen dieses Beitrags zusätzlich untersuchten Rotationen R_x um die x-Achse und R_y um die y-Achse (Bild 1) werden durch den Einsatz eines Kugelkopffräsers möglich. Dieser ermöglicht die Umorientierung um alle Achsen bei nahezu identischen Eingriffsbedingungen. Bei Schaft- und Scheibenfräswerkzeugen würde eine Umorientierung um die x- und y-Achse zu veränderten Eingriffsbedingungen führen, weswegen diese ohne weiterführende Untersuchungen nicht mit dem präsentierten Ansatz verwendet werden können. Zur genaueren Bestimmung des Effekts der Umorientierung der Frässpindel auf die Abdrängung des Werkzeugs, wurde im Rahmen dieses Beitrags eine experimentelle Identifikation der Dreh- und Kippsteifigkeit in den Gelenken vorgenommen und diese in ein Strukturmodell überführt, um anschließend simulationsgestützte Analysen zur Umorientierung der Frässpindel durchzuführen.
Experimentelle Identifikation der Nachgiebigkeit
Zur Identifikation der Nachgiebigkeit in den Gelenken wurden Zug-Druck-Versuche durchgeführt [15]. Hierbei wurde jedes Gelenk isoliert durch eine Vorrichtung in Dreh- und Kipprichtung belastet und die Winkeländerung der Gelenke mittels eines optischen Koordinatenmessgeräts aufgenommen.
Der Versuchsaufbau umfasst einen Industrieroboter des Typs IRB 4400 des Herstellers ABB, ein optisches Koordinatenmessgerät ARAMIS SRX vom Hersteller GOM und einen Kraft-Momenten-Sensor (KMS) Omega 160 der Firma ATI Industrial Automation. Zudem wurde für den Messvorgang eine Haltevorrichtung konstruiert, wie in Bild 2 zu sehen.

Bild 2: Experimenteller Aufbau zur Durchführung der Zug-Druck-Versuche an einem ABB IRB 4400 (1) mit einem optischen Koordinatenmessgerät ARAMIS SRX (2) und optischen Punkten zur Winkeldrehungserfassung (3), einem KMS (4) und einer Haltevorrichtung zur Kraftaufbringung an den Roboterflansch (5).
Die Kraft wird hierbei durch eine Gewindestange, die an dem Flansch des Roboters und über eine Konstruktion mit dem Hallenboden befestigt ist, aufgebracht. Hierfür wird der Roboter mittels bestromten Motoren auf einer Position gehalten (Bild 2) und eine auf der Gewindestange aufgebrachte Mutter zur weiteren Kraftaufbringung angezogen. Durch die an jedem Gelenk angebrachten Messlineale und die darauf aufgebrachten Messpunkte, kann so eine Drehwinkeländerung ∆φ in jedem Gelenk mit dem ARAMIS SRX Kamerasystem erfasst und in der Software ARAMIS Professional ausgewertet werden. Die währenddessen aufgebrachte Kraft wird hierbei mit dem Kraft-Momenten-Sensor am Roboterflansch aufgezeichnet und durch eine Rückwärtstransformation die wirkenden Momente in den Robotergelenken ermittelt.
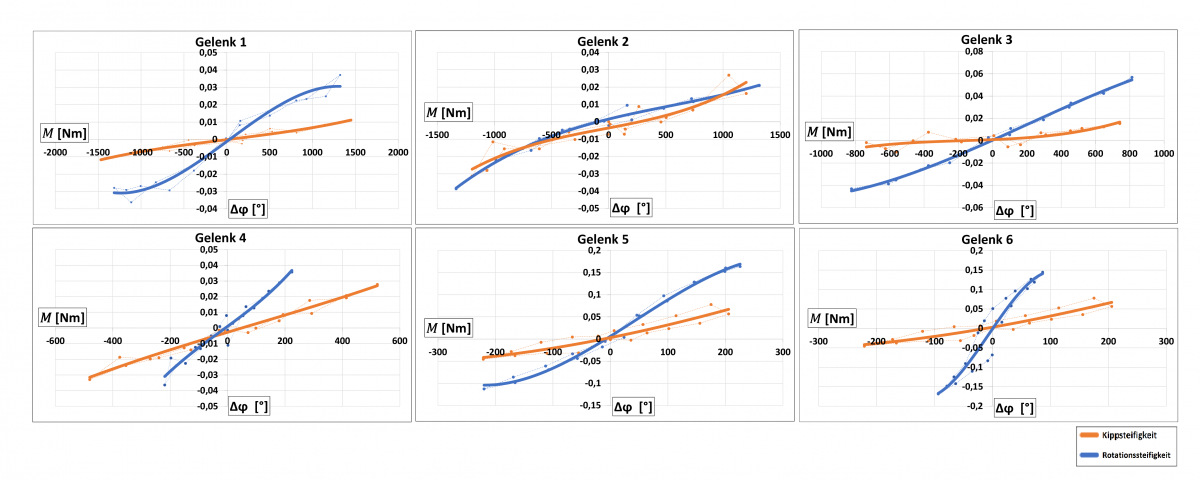
Bild 3: Nachgiebigkeitskennlinie der Rotations- und Kippsteifigkeiten aller Gelenke des Roboters.
In Bild 3 sind die Nachgiebigkeitskennlinien aller Gelenke aus den Zug-Druck-Versuchen abgebildet. Diese Nachgiebigkeitskennlinien geben die Drehwinkelveränderung in Abhängigkeit von dem aufgebrachten Drehmoment am Gelenk an. Für die Messwerte wurden polynomiale Ausgleichskurven dritten bis fünften Grades generiert, welche später dem Modell zur hinreichend genauen Systembeschreibung dienen. Im Vergleich zur Rotationssteifigkeit fällt die Kippsteifigkeit bei allen Gelenken deutlich größer aus. Bei Gelenk 6 liegt der Unterschied bei bis zu 500 %.
Strukturmodell und Steifigkeitsoptimierung
Aufbauend auf den ermittelten Nachgiebigkeitskennlinien wurde ein Strukturmodell zur Ermittlung der Abdrängung des Werkzeugpunkts, hervorgerufen durch die wirkenden Kräfte beim Fräsen, entwickelt. Das Roboterstrukturmodell lässt sich für diesen Ansatz durch folgende Gleichung darstellen:
τ=K(θ-q) (2)
Dabei ist das Gelenkdrehmoment τ abhängig von der Steifigkeitsmatrix K(θ-q) und daher von dem antriebsseitigen Gelenkwinkel θ und dem abtriebsseitigen Gelenkwinkel q. Um nun die Drehmomente in den Gelenken aus dem am Werkzeugpunkt wirkenden Kraftvektor F ⃗ berechnen zu können, wird der Ortsvektor r ⃗ vom Gelenk zur wirkenden Kraft mit dem Kraftvektor F ⃗ verrechnet. Hierbei werden die Drehmomente in Kipp- und in Drehrichtung der Gelenke getrennt berechnet. Anschließend werden die Drehwinkeländerungen ∆φ in den Gelenken aus den Nachgiebigkeitskennlinien mittels einer Transformationsmatrix ermittelt. Hierfür werden die Euler-Winkel nach der Roll-Nick-Gier-Winkel-Definition verwendet [16]. Aus diesen Gesamttransformationsmatrizen und dem Abstand des jeweiligen Gelenks zur Basis lässt sich dann die Verschiebung des Werkzeugpunkts ermitteln.
Um nun das oben beschriebene Strukturmodell zu validieren, wurden Verschiebungen an 10 charakteristischen Messpunkten (siehe Tabelle 1) in unterschiedlichen Gelenkstellungen und Belastungsrichtungen gemessen und mit den durch das Strukturmodell errechneten Werten verglichen. Die durchschnittliche Differenz zwischen Messung und Simulation der Gesamtverschiebung betrug 0,072 mm, was einer Vorhersageungenauigkeit des Modells von 4,7 % entspricht. Damit ist das Modell für die vorliegende Untersuchung hinreichend genau.
Bei der Simulation wurde zur Ermittlung der Erreichbarkeit der jeweiligen Frässpindelorientierung in RobotStudio ein Programm zur Generierung der Achsstellungen für die entsprechenden Posen entwickelt. Die wirkenden Fräskräfte wurden im Vorfeld für den entsprechenden Fall experimentell, mittels eines Kraft-Momenten-Sensors bei Fräsbearbeitungen mit einem 10 mm Kugelkopffräser in Aluminium unter Vorschub in positiver y-Richtung ermittelt.
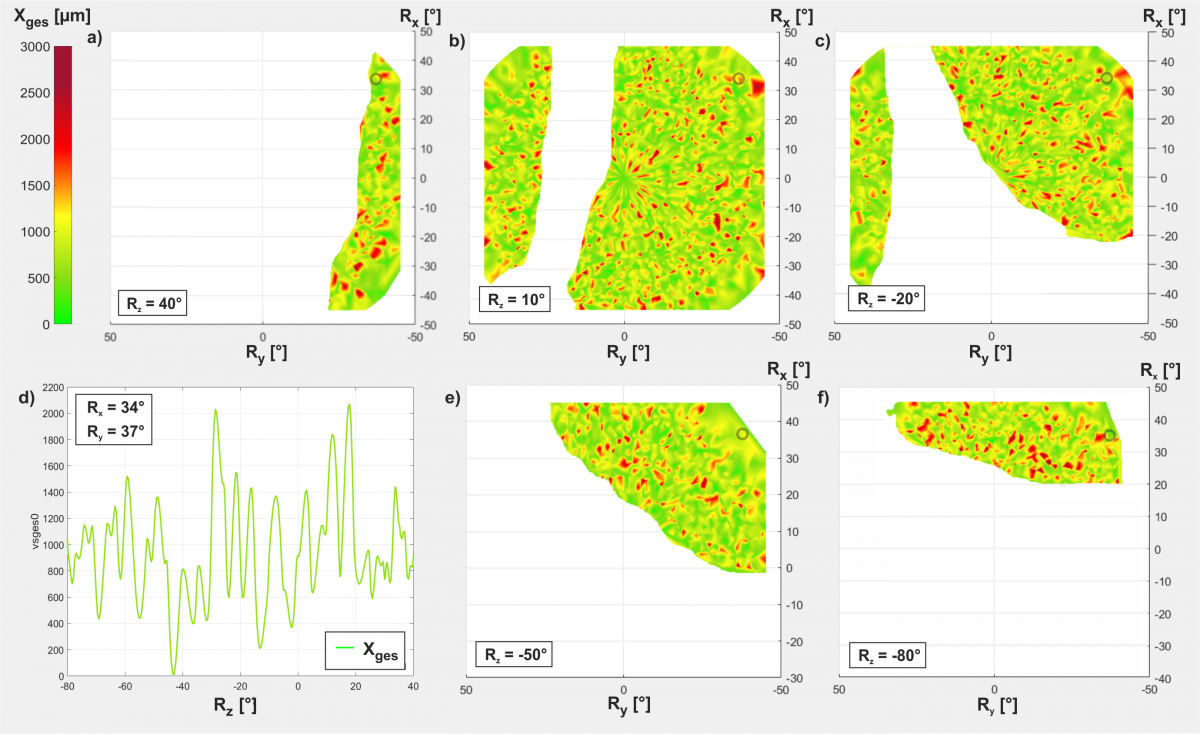
Bild 4: Simulationsergebnisse der Gesamtabdrängung des Werkzeugs x_Ges (x_Ges=√(〖x_x〗^2+〖x_y〗^2+〖x_z〗^2 ); an der Position x=1454, y=195, z=760) in Abhängigkeit der Änderung der Orientierungen R_x und R_y des Werkzeugs um ±50° bei diskreten Werten für R_z (a), b), c), e) und f)); Gesamtabdrängung des Werkzeugs bei einer fixen Orientierung von R_x=34°, R_y=37° in Abhängigkeit von R_z (d)).
Mittels dieses Strukturmodells wurde, zur Untersuchung der Abhängigkeit der Abdrängung von der Orientierung des Werkzeugs, eine Berechnung der Verschiebungen an einem exemplarischen Punkt durchgeführt. Die Ergebnisse dieser Berechnung sind in Bild 4 dargestellt. Hierfür wurde an einer definierten Position und in einer wie in Bild 1 dargestellten Ausgangsorientierung die Gesamtabdrängung x_Ges des Werkzeugs ermittelt. Ausgehend von dieser Ausgangsorientierung wurde in diskreten Schritten von 1° das Werkzeug in den Orientierungen R_x, R_y und R_z umorientiert. Bild 4 zeigt die Gesamtverschiebung x_Ges bei der entsprechenden Orientierung der Frässpindel in Abhängigkeit von R_x und R_y, bei einer jeweiligen Orientierung von R_z = 40°, 10°, -20°, -50° und -80°. Es lässt sich eine starke nichtlineare Abhängigkeit der Abdrängung von der Spindelorientierung erkennen. Die Gesamtabdrängung x_Ges in Abhängigkeit von R_x, R_y und R_z beträgt bis zu 2,201 mm und minimal 0,039 mm. Zusätzlich wurde bei fixen Winkeln R_x=34° und R_y=37° die Veränderung der Gesamtverschiebung in Abhängigkeit von R_z dargestellt (Bild 4, links unten). Hierbei lässt sich eine minimale Verschiebung von 0,091 mm (R_z=42°) und eine maximale Verschiebung von 1,620 mm (R_z=24°) erkennen. Insgesamt lässt sich somit ein starker Einfluss von allen Rotationsrichtungen auf die Gesamtabdrängung x_Ges nachweisen. Diese Abhängigkeit kann zur Kompensation der Abdrängung des Werkzeugpunkts genutzt werden, indem die Orientierung der Frässpindel bei der Bahnplanung mittels des vorgestellten Strukturmodells optimiert wird.
Zusammenfassung und Ausblick
Die vorliegende Arbeit thematisiert einen Ansatz zur Minimierung der Werkzeugabdrängung bei robotergestützten Fräsprozessen, welcher sich durch die Ausnutzung der drei rotatorischen Freiheitsgrade des Fräswerkzeugs ergibt. Die entsprechenden redundanten Achskonfigurationen dienen hierbei der Minimierung der Abdrängung. Aufgrund der deutlichen Unterschiede in der Dreh- und Kippsteifigkeit in allen Gelenken ist ein Unterschied in der Werkzeugabdrängung in Abhängigkeit von der Werkzeugorientierung nachgewiesen worden. Hierfür wurden zunächst Zug-Druck-Versuche durchgeführt und diese Ergebnisse in ein Strukturmodell überführt. Durch Simulationen anhand dieses Modells konnten die zu erwartenden Verschiebungen des Werkzeugs an einem exemplarischen Punkt und bei unterschiedlichsten Orientierungen von R_x, R_y und R_z des Werkzeugpunkts nachgewiesen werden. Hierbei konnte eine Differenz der Gesamtabdrängung ∆x_Ges in Abhängigkeit von der Spindelorientierung von mehr als 2,1 mm identifiziert werden. Neben den bereits in der Literatur untersuchten Methoden zur Optimierung der Werkzeugabdrängung durch Änderung der Orientierung R_z, lassen die Ergebnisse dieses Papers auf ein hohes Potenzial bei der Umorientierung von R_x und R_y schließen. Zukünftig sollten die simulierten Ergebnisse durch Fräsversuche validiert und das Modell um eine dynamische Betrachtung der Roboterstruktur erweitert werden. Zur Generierung einer sinnvollen Trajektorie gilt es darüber hinaus die gesamte abzufahrende Bahn und die mit der Umorientierung zusammenhängenden Ungenauigkeiten der einzelnen Punkte auf der Bahn, sowie die maximal zulässigen Gelenkwinkeländerungen zu betrachten.
Schlüsselwörter:
Fräsen, Industrieroboter, Koordinatenmessgerät, Materialbearbeitung, Steifigkeit, Werkzeugorientierung, Freiheitsgrade
Literatur:
[1] Plyusnina, M.; Krewet, C.; Rieger, M.; Bickendorf, J.; Kuhlenkötter, B. (Hrsg): In-Prozess-Erfassung und Auswertung prozessdefinierender Kennwerte beim robotergestützten Polieren von Designoberflächen. Dortmund: Tagungsband. Dresden: Technische Universität 2015.
[2] Möllensiep, D.; Gorlas, T.; Kulessa, P.; Kuhlenkötter B.: Real-time stiffness compensation and force control of cooperating robots in robot-based double sided incremental sheet forming. Production Engineering 15 (2021) 5, S. 683-699.
[3] Penczek, L. N.; Krampe, M.; Kuhlenkötter, B.: Analysis of surface quality during milling with industrial robots as a function of axis. CPSL 2nd Conference (2021), S. 1-10.
[4] Pan, Z.; Zhang, H.; Zhu, Z.; W. J.: Chatter analysis of robotic machining process. Journal of Materials Processing Technology 173 (2006) 3, S. 301-309.
[5] Abele, E.; Bauer, J.; Stelzer, M.; Stryk, O.: Wechselwirkungen von Fräsprozess und Maschinenstruktur am Beispiel des Industrieroboters. Entwicklung von Modellkomponenten für eine Offlinekompensation der spanenden Bearbeitung mit Industrierobotern (2008), S. 733-737.
[6] Zäh, M. F.; Roesch O.: Improvement of the Static and Dynamic Behavior of a Milling Robot. International Journal of Automation Technology 9 (2015) 2, S. 129-133.
[7] Beyer, L.: Genauigkeitssteigerung von Industrierobotern. Insbesondere mit Parallelkinematik. Forschungsberichte aus dem Laboratorium Fertigungstechnik / Helmut-Schmidt-Universität, Universität der Bundeswehr Hamburg, Bd. 1. Aachen 2005.
[8] Rosenbauer, T.: Getriebe für Industrieroboter. Beurteilungskriterien, Kenndaten, Einsatzhinweise. Zugl.: Aachen, Univ., Berichte aus der Produktionstechnik, Bd. 94,32. Aachen 1995.
[9] Zäh, M. F.; Rösch O.: Steigerung der Arbeitsgenauigkeit bei der Fräsbearbeitung mit Industrierobotern. Zeitschrift für wirtschaftlichen Fabrikbetrieb 106 (2011) 9, S. 658-662.
[10] Möller, C.; Schmidt, C. S.; Shah, N. H.; Wollnack, J.: Enhanced Absolute Accuracy of an Industrial Milling Robot Using Stereo Camera System. Procedia Technology 26 (2016), S. 389-398.
[11] Rösch, O.: Steigerung der Arbeitsgenauigkeit bei der Fräsbearbeitung metallischer Werkstoffe mit Industrierobotern. Zugl.: München, Techn. Univ., Diss., 2014.
[12] Celikag, H.; Sims, N. D.; Ozturk, E.: Cartesian Stiffness Optimization for Serial Arm Robots. Procedia CIRP 77 (2018), S. 566-569.
[13] Posada, D.; Schneider, U.; Sridhar, A.; Verl, A.: Automatic Motion Generation for Robotic Milling Optimizing Stiffness with Sample-Based Planning. Machines 5 (2017) 1, S. 3.
[14] Schneider, U.; Posada, D.; Ricardo, J.; Verl, A.: Automatic pose optimization for robotic processes. 2015 IEEE International Conference on Robotics and Automation (ICRA). IEEE 52015, S. 2054-2059.
[15] Bauer, J.: Methoden der Offline-Bahnkorrektur für die spanende Bearbeitung mit Industrierobotern. Zugl.: Darmstadt, Techn. Univ,. Schriftenreihe des PTW. Berlin 2011.
[16] Ang, M.; Tourassis, V.: Singularities of Euler and Roll-Pitch-Yaw Representations. IEEE Transactions on Aerospace and Electronic Systems AES-23 (1987) 3, S. 317-324.




